앞에서 int 형의 저장에 대해서 살펴보았다.
이제 부동소수 표현방식에 대해서 살펴보겠다.
부동소수 표현 방식은 4바이트의 경우
1 bit 부호 | 8bit 지수부 | 23 bit 가수부
로 나누어져 있다.
0|000 0000 0|000 0000 0000 0000 0000
로 표현되어 지는데.
지수부 표현방식은 2의 지수승으로 표현된다. 지수승 표현은 8bit 계산값 n 에서 127을 뺀값을 지수승 하는 방식이다.
예를 들어, 011 1111 1 일 경우 127이므로 127 - 127 =0 이 되므로 지수표현은 2의 0승 즉 1이 된다.
그다음 가수부 표현은 첫번째 bit 1/2
두번째 bit 1/4
이런식으로 계산하게 된다.
이 방식으로 1.0을 표현하면,
0|011 1111 1|000 0000 0000 0000 0000 0000 이 되고 이걸 16진수로 표현하면
3 f 8 0 0 0 0 0즉,
3f800000 가 된다.
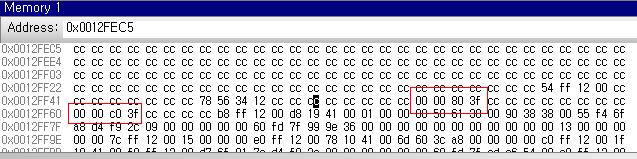
실제 프로그램에서 메모리에는 위치가 반대로 되므로
00 00 80 3f 이런식으로 잡힐것이다.
같은 방식으로 1.5 는
3f c0 00 00 가 될 것이다.
이제 부동소수 표현방식에 대해서 살펴보겠다.
부동소수 표현 방식은 4바이트의 경우
1 bit 부호 | 8bit 지수부 | 23 bit 가수부
로 나누어져 있다.
0|000 0000 0|000 0000 0000 0000 0000
로 표현되어 지는데.
지수부 표현방식은 2의 지수승으로 표현된다. 지수승 표현은 8bit 계산값 n 에서 127을 뺀값을 지수승 하는 방식이다.
예를 들어, 011 1111 1 일 경우 127이므로 127 - 127 =0 이 되므로 지수표현은 2의 0승 즉 1이 된다.
그다음 가수부 표현은 첫번째 bit 1/2
두번째 bit 1/4
이런식으로 계산하게 된다.
이 방식으로 1.0을 표현하면,
0|011 1111 1|000 0000 0000 0000 0000 0000 이 되고 이걸 16진수로 표현하면
3 f 8 0 0 0 0 0즉,
3f800000 가 된다.
실제 프로그램에서 메모리에는 위치가 반대로 되므로
00 00 80 3f 이런식으로 잡힐것이다.
같은 방식으로 1.5 는
3f c0 00 00 가 될 것이다.
